Robert A McDougal

Matlab Examples

Matlab is a program by The Mathworks for scientific computing.

Outline of Contents

• Plotting Points in 3-Space
• Saving Animations
• Matlab Events
• Parallel Computing

Plotting Points in 3-Space

scatter3 lets you make a scatter plot. You can specify the color and point size for each point.

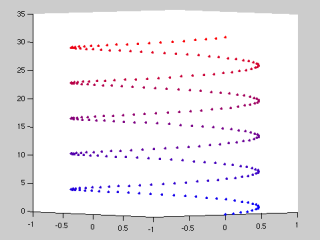
The above helix was plotted using graphHelix.m:

function graphHelix
  t=linspace(0,10*pi,255);

  % make t a column vector
  t=t(:);

  % display in a new window
  figure

  % to fade between two colors, we take a convex combination of the two
  red=[1 0 0];
  blue=[0 0 1];

  x=sin(t);
  y=cos(t);
  frac=t/(10*pi);
  color=frac*red+(1-frac)*blue;

  scatter3(x,y,t,30,color,'filled');
end

Saving Animations

The following function, makeAvi.m rotates the current 3-d image and saves the rotation as a .avi file. The .avi file will be quite large, but you can then encode it into other formats. Here, for example, I encoded it into a .flv file.

% makeAvi(filename,rotations)
%
% makes an avi of the current 3d figure being rotated 360 degrees
% rotations times. If no filename is specified, uses output.avi
function makeAvi(filename,rotations)
  if nargin<1
    filename='output.avi';
  end
  if nargin<2
    rotations=1;
  end

  % fix aspect ratio
  axis vis3d;

  % create file
  movie=avifile(filename,'fps',30,'compression','none');

  for i=1:(360*rotations)
    view([i 10]);
    drawnow;
    disp(sprintf('%d',i));

    movie=addframe(movie,gcf);
  end

  movie=close(movie);
end

Matlab Events

The function odeEventDemo.m demonstrates numerical integration with events in Matlab:

function odeEventDemo(tStop)
  if nargin <1
    tStop=20;
  end
 
  y0=0;

  [t,y]=integrateWithEvent(@theOde, 0, tStop, y0, @myEvent, @myOnEvent);

  plot(t,y);

  function [t,y]=integrateWithEvent(fn, tstart, tstop, y0, event, onEvent)
    t=[];
    y=[];
    tStart=tstart;
    while true
      [tPrime, yPrime]=ode45(fn, [tStart, tstop], y0, odeset('Events',event));
      t=[t;tPrime];
      y=[y;yPrime];
      num=length(tPrime);
      y0=yPrime(num,:);
      if (tPrime(num)>=tstop)
        break;
      else
        tStart=tPrime(num);
        y0=onEvent(tStart,y0);
      end
    end
  end

  % resets y to zero whenever the event occurs
  function result=myOnEvent(t,y)
    result=0;
  end

  function dy=theOde(t,y)
    dy=y+1;
  end

  function [value,isterminal,direction]=myEvent(t,y)
    value=y-4;
    direction=1;
    isterminal=1;
  end
end

Parallel Computing

The demo code compares linear, quadratic, and cubic growth. A title, legend, and axis labels are provided. The y-axis is also scaled manually.

function parForDemo
  % check for parallel computing toolbox
  supportsParallel=false;
  try
    sizePool=matlabpool('size');
    supportsParallel=true;
    if sizePool==0
      disp('Warning: It looks like your computer has the parallel computing')
      disp('toolbox, but no parallel pool is available. Type ''matlabpool''')
      disp('to start a pool to enable faster basin of attractions calculations');
    end
  catch
  end

  % setup for the calculation
  x=linspace(0,5);
  y=zeros(length(x),3);

  % the calculation.
  if supportsParallel
    parfor i=1:3
      disp(i);
      y(:,i)=x.^i;
    end
  else
    for i=1:3
      disp(i);
      y(:,i)=x.^i;
    end
  end
  plot(x, y(:,1), 'red', x, y(:,2), 'blue', x, y(:,3), 'black');
  title('Comparison of growth rates');
  legend('linear', 'quadratic', 'cubic');
  xlabel('x');
  ylabel('y');
  ylim([0 50]); % set the y-range
end